 С позиций биомеханики движения фигуриста могут быть разделены на две основные группы движений: в обязательных фигурах и в произвольном катании (включая парное катание и танцы на льду). В основе такого разделения лежит несовпадение двигательных задач и, как следствие, существенное различие кинематических, динамических и информационных характерстик этих групп движений. С позиций биомеханики движения фигуриста могут быть разделены на две основные группы движений: в обязательных фигурах и в произвольном катании (включая парное катание и танцы на льду). В основе такого разделения лежит несовпадение двигательных задач и, как следствие, существенное различие кинематических, динамических и информационных характерстик этих групп движений.
Так, скорость скольжения в обязательных фигурах колеблется в диапазоне 1—2,5 м/с в больших фигурах и около 1 м/с в фигурах с петлями. В произвольном катании скорость скольжения может достигать 8 м/с и более. Параметры вращательных движений также различны.
Сравнение динамических характеристик движений в обязательных фигурах и в произвольном катании также говорит о. значительном различии этих двух групп движений.
Показательно в этом плане, что фигуристов можно разделить на две группы: одним лучше удаются обязательные фигуры, другим — произвольное катание. В основе этого разделения обычно лежат особенности нервной системы спортсмена, по-видимому имеющие связь с процессами управления движениями. Те, кому больше удается школа, как правило, пунктуальны, флегматичны и осторожны. Любители произвольного катания более возбудимы, эмоциональны, артистичны, смелы.
Обязательные фигуры. Анализ различных приемов выполнения обязательных фигур, сравнение их эффективности в практике тренировок и в соревновательной деятельности позволяют считать, что одним из основных направлений совершенствования этой группы движений является стремление к сдержанной, лаконичной манере исполнения. Подтверждение справедливости такого подхода— трансформация стиля выполнения обязательных фигур с момента их зарождения до наших дней. Эволюция стиля проявляется в уменьшении амплитуды движений свободной и опорной ноги, уменьшении скорости скольжения, ослаблении силы толчка и резкости движений, уменьшении толщины и глубины следа и т. п.
У начинающих фигуристов, спортсменов, не обладающих совершенной техникой, часто можно видеть расслабленное туловище, болтающиеся руки и свободную ногу. Это осложняет задачу управления движением, препятствует сохранению непрерывности следа. В практике встречаются и противоположные ошибки: чрезмерное напряжение, закрепощение излишне большого числа звеньев тела, что в конечном итоге приводит к увеличению усилий между коньком и льдом, скоблению льда, затрат энергии, т. е. к аналогичным негативным последствиям, затрудняющим непрерывность выполнения движений.
Произвольное катание. Главной задачей обучения фигуриста является не столько сообщение телу движения, что в принципе не столь уж сложно, сколько овладение искусством управлять движением в процессе скольжения, что, как показывает практика, представляет основную трудность.
Известно, что качество шагов в произвольной программе в большой степени определяется реберностью их исполнения. Действительно, при скольжении на плоскости конька увеличивается площадь опоры, уменьшается удельное давление, что приводит к ухудшению скольжения конька по льду, так как увеличивается сила трения. Скольжение на ребрах коньков выполняется естествен-
но только при движении по кривой, вот почему показателем мастерства катания считается крутизна дуг, которая создает дополнительную возможность для увеличения скорости движения путем разгибания ноги в условиях одноопорного скольжения. -
Двигательная задача фигуриста при выполнении вращений — управление приобретенным вращательным движением путем сокращения и расслабления мышц при приближении и удалении звеньев тела от оси вращения. В прыжках разгибание толчковой ноги и маховые движения в толчке должны выполняться так, чтобы преобразовать часть энергии скольжения в энергию вращательного движения вокруг продольной оси и сообщить телу движение вперед-вверх.
В парном катании в элементах, выполняемых раздельно, действуют те же закономерности, а в совместных элементах особое значение приобретает рациональное взаимодействие между партнерами.
СКОЛЬЖЕНИЕ ПО ДУГЕ
Скольжение фигуриста по дуге в одноопорном положении является основным режимом движения и характеризуется такими величинами, как скорость, ускорение, радиус дуги скольжения, сила инерции, сила давления конька на лед, сила трения. Для того чтобы определить, как они связаны, рассмотрим схему одноопорного скольжения (рис. 4).
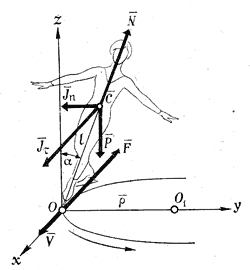 |
| Рис. 4. Силы, действующие на фигуриста при одноопорном скольжении |
На тело фигуриста, скользящего по. дуге окружности радиусом ρ, имеющего в данный момент скорость V, действуют: сила веса Р, сила трения F, направленная в сторону, противоположную движению; касательная сила инерции Jτ, параллельная оси Ох и направленная противоположно замедлению; нормальная (центробежная) сила инерции Jn, параллельная оси Оу; опорная реакция N, равная давлению фигуриста на лед и направленная по продольной оси вверх.
В рассматриваемый момент тело фигуриста находится в координатной плоскости zOy, продольная ось наклонена на угол а к вертикали: l — расстояние от о.ц.т. тела до точки опоры О.
Составив уравнения равновесия сил и моментов и преобразовав их, получим шесть уравнений, анализируя которые можно сделать ряд важных практических выводов.
Важной характеристикой скольжения является наклон продольной оси тела к поверхности льда. Он определяет реберность скольжения — одно из основных условий высокого качества выполнения всего комплекса элементов фигурного катания.
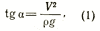
где ρ — радиус кривизны следа.
В формулу не входит масса тела. Отсюда первый вывод: угол наклона продольной оси тела фигуриста зависит только от величины радиуса дуги и скорости скольжения.
Из формулы (1) можно сделать и другой вывод: угол наклона продольной оси увеличивается пропорционально квадрату скорости скольжения и 'уменьшается с увеличением радиуса дуги скольжения.
Известно, что при малых углах наклона опорная нога может оставить на льду двухреберный след, а это грубая ошибка.
Формула (1) связывает между собой четыре величины. Каждую из них можно выразить через остальные. Интерес представляют выражения для скорости скольжения (2) и радиуса дуги скольжения (3).

При изучении техники скольжения полезно знать выражение силы взаимодействия конька со льдом.
Величина давления конька опорной ноги на лед определяется формулой:

Так как косинус угла всегда меньше единицы, то из формулы (4) следует вывод: при скольжении по дуге в состоянии динамического равновесия давление конька на лед всегда больше веса фигуриста и равно ему при скольжении по прямой.
Для более детального анализа зависимости величины давления конька на лед воспользуемся следующим соотношением:
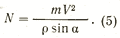
Как видим, давление на лед зависит от массы тела фигуриста, квадрата скорости, радиуса дуги скольжения и синуса угла наклона продольной оси тела фигуриста. Давление возрастает с увеличением массы тела фигуриста и скорости его скольжения и убывает с увеличением радиуса дуги и угла наклона продольной оси тела.
Сложность выполнения обязательных фигур, особенно в форме восьмерки, заключается в сохранении такой скорости скольжения, которая обеспечивает реберность и достаточно высокое качество поворотов на протяжении всей фигуры. Рассмотрим причины, вызывающие замедление скольжения при условии, что фигурист не сгибает и не разгибает опорную ногу. Кроме силы сопротивления воздуха тормозящей силой при скольжении является сила трения. Связь величины замедления с коэффициентом трения конька о лед может быть выражена следующим образом:
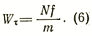
Ясно, что при одноопорном скольжении замедление прямо пропорционально давлению на лед, коэффициенту трения и обратно пропорционально массе тела.
В ряде случаев удобнее воспользоваться другой формулой (6).
Поскольку  . то после преобразования получаем: . то после преобразования получаем:
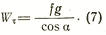
Так как на практике величина cos а меняется незначительно, а ускорение силы тяжести g — величина постоянная для данного места, то замедление зависит главным образом от коэффициента трения конька опорной ноги о лед.
Коэффициент трения скольжения зависит от многих причин: от качества льда, его температуры и состава воды, от материала, из которого сделано лезвие конька, и заточки. Чем ниже температура льда, тем больше коэффициент трения. Лед, полученный из жесткой воды, создает большее сопротивление скольжению, чем лед из мягкой воды. При низкой температуре лед тверже, а при повышенной мягче. В первом случае скольжение затрудняется из-за твердости льда, а во втором — из-за того, что лезвие конька глубоко врезается в мягкий лед.
Коэффициент трения на хорошем льду минимален, значит, и замедление при скольжении меньше. Коэффициент трения стали о лед колеблется в пределах 0,01—0,03.
Измерения показывают, что при выполнении круга вперед-наружу средние величины скорости на каждой четверти окружности равняются: V1 = 2,2 м/с, V2=l,87 м/с, V3=1,55 м/с, V4= 1,34 м/с.
Как видим, характер уменьшения скорости соответствует рав-нозамедленному движению. Другими словами, у квалифицированных фигуристов замедление при простом скольжении по дугам практически постоянно.
При выполнении сложных фигур (простая восьмерка со скобками, восьмерка с двукратными тройками и особенно восьмерка назад с тройкой) характер падения величины скорости скольжения нелинейный. В первой половине фигуры уменьшение скорости скольжения незначительно, однако во второй половине начинает проявляться следующая зависимость: уменьшение скорости скольжения вызывает уменьшение угла наклона конька ко льду и переход к скольжению на плоскости конька. Отсюда как следствие увеличивается площадь опоры и сила трения. В результате при выполнении сложных фигур скольжение фигуриста не равноза-медленно и скорость убывает нелинейно. Чем ниже квалификация спортсмена, тем ярче выражена нелинейность, тем сильнее замедление в конце фигуры.
У фигуристов высокого, класса благодаря качественному реберному скольжению, отсутствию скобления льда в поворотах и умению набирать ход падение скорости от начала фигуры к концу выражено слабее.
ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ ФИГУРИСТА
Для более полного представления о движении фигуриста при скольжении по дуге рассмотрим схему, приведенную на рис. 5. Из схемы видно, что точки тела, расположенные на разном расстоянии от центра круга, имеют разные величины линейной скорости движения. Это означает, что во время скольжения по окружности фигурист вращается вокруг оси, проходящей через центр окружности. Нетрудно подсчитать величину угловой скорости вращения тела со за время выполнения одного круга конек опорной ноги совершает один оборот, т. е. поворот на 360°. Значение угловой скорости вращения тела в больших фигурах составляет около 0,1 об/с, в петлевых — около 0,3— 0,5 об/с, а в самой петле — около 0,6—0,8 об/с. Другими словами, при скольжении по дуге тело фигуриста участвует во вращательном движении.
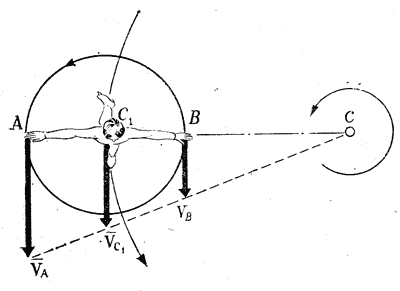 |
| Рис. 5. Схема движения тела фигуриста при скольжении по окружности |
В обязательных упражнениях встречаются также разновидности опорных вращательных движений в виде поворотов и петель. В этих элементах основу составляет встречный поворот верхней части' тела относительно нижней. В произвольном же катании наиболее характерны движения, связанные с вращением всего тела вокруг продольной оси. Так, во вращениях и комбинациях вращений число оборотов достигает нескольких десятков, а скорость — до 2 об/с.
В прыжках вращение происходит в безопорных условиях и достигает максимальной скорости (до 4,5 об/с).
В связи с особой важностью вращательных движений приведем некоторые упрощенные положения механики вращательного движения фигуриста вокруг вертикальной оси. Величина угловой скорости определяется отношением угла поворота тела к времени, за которое произошел поворот:

Угловая скорость характеризуется не только величиной, но и направлением в пространстве, т. е. является вектором, направленным по оси вращения в ту сторону, откуда вращение наблюдается против часовой стрелки. Различают среднюю угловую скорость, измеряемую в течение нескольких оборотов, и мгновенную угловую скорость, т. е. скорость вращения в данный момент.
Если угловая скорость всех точек тела одинакова, то линейная скорость для каждой точки разная. Зависимость между угловой и линейной скоростями точки выражается формулой:

где R — расстояние точки от оси вращения.
Эта простая зависимость имеет во вращениях важное значение, так как при одной и той же угловой скорости тела линейные скорости точек тела разные: чем дальше они отстоят от оси вращения, тем их линейная скорость больше.
Момент инерции. Мерой инертности тела при поступательном движении является его масса. Во вращательном движении особое значение приобретает распределение массы тела относительно оси вращения: удаление массы от оси вращения увеличивает инертность тела, а приближение к оси уменьшает.
Мерой инертности тела во вращательном движении является момент инерции, равный сумме произведений масс частей тела на квадраты их расстояний до оси вращения:

где mi — массы частей тела; ri— расстояние масс тела до оси вращения.
Следует подчеркнуть, что в выражение для величины момента инерции входят расстояния масс частей тела до оси вращения во второй степени, что объясняет значительное изменение момента инерции тела с постоянной массой при перераспределении масс частей тела относительно оси вращения.
Важной характеристикой вращающегося тела является количество запасенного им вращательного движения. Она носит название момента количества движения тела К. Величина момента количества Движения вращающегося тела измеряется произведением момента инерции тела относительно оси / и угловой скорости вращения тела вокруг этой оси:

Момент количества движения является характеристикой, свойственной вращательному движению.
Закон сохранения момента количества движения. Вращающееся тело стремится сохранить количество приобретенного вращательного движения, или, другими словами, величину момента количества движения.
Во вращательном движении без учета сил трения при выполнении пируэта зависимость I·ω = const проявляется в постоянной взаимосвязи между величинами момента инерции тела и его угловой скоростью вращения. Другими словами, уменьшение одного множителя вызывает увеличение другого настолько, что их произведение остается неизменным. Именно поэтому приближение звеньев тела к оси вращения в процессе группировки, т. е. уменьшение момента инерции, обусловливает увеличение скорости вращения тела и наоборот.
Сравнение моментов инерции тела в различных положениях позволяет, в частности, установить, что группировка рук из положения в стороны может увеличить скорость вращения тела почти вдвое, а переход из положения «ласточка» в положение стоя с руками вдоль тела — более чем в шесть раз. Эти данные не учитывают сил сопротивления, испытываемых телом при вращении, поэтому реальное увеличение угловой скорости всегда меньше и зависит от характера контакта конька со льдом. С этой точки зрения выгодны опора на переднюю треть конька без касания льда зубцами и скобления конька о лед. Наименьшее сопротивление оказывается в том случае, если конек опорной ноги во время вращения выполняет петли небольшого размера (3—5 см).
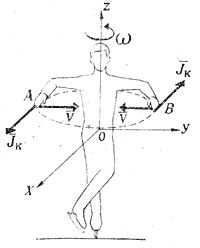 |
| Рис. 6. Силы инерции Кориолиса, действующие на точки вращающегося тела при группировке |
Причины изменения скорости вращения. В различных вращательных движениях и пируэтах фигурист меняет угловую скорость вращения в значительных пределах. Изменение скорости вращения вызывают внутренние силы —группировки и разгруппировки, т. е. силы активного действия,, обусловленные мышечной деятельностью человека. Не трудно убедиться, что линии действия этих сил направлены к оси вращения или от нее, т. е, они не участвуют во вращении. Какие же силы непосредственно ускоряют или замедляют вращение тела? Это силы инерции Ко-риолиса, или, говоря точнее, моменты этих сил. Рассмотрим физическую сущность возникновения сил инерции Корио-лиса, определим направление их действия и приведем формулу для определений величины этих сил (рис. 6).
В пируэте при группировке и разгруп-пировке имеют место два движения: вращение тела и движение рук и свободной ноги вдоль радиуса к оси или от нее. Когда руки подтягиваются к оси вращения, линейные скорости их частей становятся меньше, т. е. звенья тела, участвующие в группировке, приобретают отрицательное ускорение (Кориолисово), иными словами, ускорение, направленное против вращения. Так как всякая сила инерции всегда направлена в сторону, противоположную ускорению, то силы инерции Кориолиса будут направлены по ходу вращения. Они приложены к частям тела, выполняющим группировку, направлены в сторону вращения и увеличивают его угловую скорость.
Итак, в процессе вращения тела, перемещения рук и свободной ноги к оси вращения или от нее возникают силы инерции Кориолиса, которые ускоряют вращение при группировке и замедляют его при разгруппировке. Силы инерции зависят от величины угловой скорости вращения тела ω, линейной скорости частей тела при группировке и разгруппировке V, их массы m, а также от синуса угла β между векторами ω и V. Величина этих сил определяется по формуле:

Применение основных положений механики вращательных движений позволяет сделать важные практические выводы, разъясняющие некоторые ключевые детали техники выполнения обязательных фигур. Принципиальным вопросом изучения техники поворотов является определение причины, вызывающей смену фронта скольжения. Известно, что вращение какого-либо звена тела в одном направлении вызывает поворот других частей тела в противоположном направлении.
В поворотах обязательных фигур верхняя часть тела— плечи, руки, голова — выполняет так называемое обратное движение, т. е. поворот перечисленных звеньев относительно таза. Это движение вызывает соответствующий поворот нижней части тела в противоположном направлении. При достаточной амплитуде и скорости встречного вращения верхней части тела относительно нижней последняя вместе с коньком меняет фронт своего движения, т. е. совершает поворот на угол, близкий к 180°.
Таким образом, механизм вращательного компонента поворотов заключается во встречном вращении верхней части тела относительно нижней.
ДВИЖЕНИЕ ТЕЛА В ПОЛЕТЕ
Анализ кинограмм показывает, что в хорошо выполненном прыжке движение оси вращения тела близко к поступательному. В результате сложное движение тела в полете можно рассматривать как движение поступательное вместе с осью вращения и вращательное вокруг этой оси (рис. 7). Известно, что при поступательном движении все точки тела в определенный момент имеют одинаковые векторы скоростей и ускорений. Следовательно, исследование движения оси вращения можно заменить исследованием движения точки. В качестве такой точки удобно выбрать о. ц. т. тела, через который на протяжении всего безопорного периода проходит ось вращения.
Следует отметить, что разложение сложного движения на поступательное и вращательное является исследовательским приемом, в' то время как в действительности оба движения тесно связаны и представляют собой две стороны единого процесса.
 |
| Рис. 7. Разложение сложного движения тела в полете на поступательное и вращательное |
Поступательное движение тела. Уравнение движения центра тяжести тела, брошенного под углом к горизонту, в проекциях на оси координат х и у без учета сопротивления воздушной среды выглядит следующим образом:

где α0 — угол вылета; V0 — начальная скорость вылета; g — ускорение свободного падения.
Уравнение показывает, что форма траектории, а следовательно, и максимальная высота и дальность прыжка зависят лишь от начальных параметров движения о. ц. т. тела: начальной скорости вылета и угла вылета при постоянном ускорении свободного падения.
Таким образом, траектория движения о. ц. т. тела в безопорном периоде определяется лишь начальными условиями — по форме это парабола. Никакими вращениями конечностей, их перемещениями и т. п. изменить траекторию движения о. ц. т. в полете нельзя.
Отсюда вытекает важный практический вывод: характер движения о. ц. т. тела в безопорном периоде целиком определяется начальными условиями вылета.
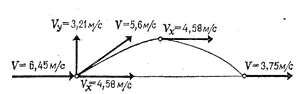 |
| Рис. 8. Траектория движения центра тяжести тела в полете |
На рис. 8 приведена траектория движения о. ц. т. тела в полете при выполнении прыжка двойной лутц. Как видим, после выполнения стопорящего движения в начале полета горизонтальная составляющая скорости о. ц. т. тела равна 4,58 м/с, а возникшая в результате толчка и стопора вертикальная составляющая скорости — 3,21 м/с, что обеспечило подъем -о. ц. т. тела в наивысшей точке на 0,525 м.
Угол вылета при этом составил 35°. В безопорном периоде, двигаясь с постоянной горизонтальной скоростью, равной 4,58 м/с, фигурист пролетел 2,86 м за 0,626 с. При этом вертикальная составляющая скорости уменьшалась с 3,21 м/с при вылете до нуля в верхней точке полета и затем к моменту приземления вновь достигла 3,21 м/с.
Интересно отметить, что перед толчком фигурист имел горизонтальную скорость 6,45 м/с, а после толчка, в результате стопорящего движения, горизонтальная составляющая скорости равнялась 4,58 м/с. Таким образом, потеря горизонтальной скорости в результате толчка составила 1,87 м/с. Такие же потери происходят и при приземлении. Если в полете горизонтальная скорость тела была равна 4,58 м/с, то после приземления скорость скольжения составила 3,75 м/с. В итоге потеря горизонтальной составляющей при приземлении 0,83-м/с.
Общие потери горизонтальной составляющей скорости в толчке и приземлении составили 2,7 м/с, т. е. 41,86% величины скорости перед толчком.
Вращение тела в полете. Характер вращательного движения тела в полете существенно влияет на качество выполнения прыжка. И недостаточный и чрезмерный поворот тела в полете затрудняет приземление. Для анализа вращательного движения тела в полете можно воспользоваться законом сохранения момента количества движения. Фигурист в полете выполняет группировку и разгруппировку, т. е. определенным образом перемещает звенья тела относительно оси вращения, чем изменяет момент инерции тела.
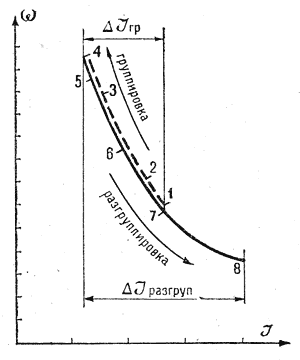 |
| Рис. 9. Изменение угловой скорости вращения тела в полете |
На рис. 9 дан график изменения угловой скорости в прыжке в 2,5 оборота. Точки 1, 2, 3 соответствуют группировке, точка 4 — фиксация группировки, точки 5, 6, 7 и 8 — разгруппировке.
График иллюстрирует характер изменения скорости вращения тела в полете в результате группировки и раз-группировки звеньев тела. Характер кривой показывает, что наиболее значительный прирост угловой скорости вращения тела происходит в положениях, близких к положению наиболее плотной группировки.
При рассмотрении вращательного движения в полете очень важно определить влияние величины момента количества движения на параметры вращательного движения. Чем больше момент количества движения, которым обладает тело,, или, другими словами, чем большее количество вращательного движения приобретено фигуристом в толчке, тем при одинаковой плотности группировки больше угловая скорость вращения.
Итак, скорость вращения тела фигуриста в полете определяется кинетическим моментом, приобретенным в толчке, и движениями в полете — группировкой и разгруппировкой.
Сравнение величины скорости вращения в прыжках говорит о том, что увеличение числа оборотов сопровождается увеличением начальной угловой скорости вращения тела при отрыве. В двойных прыжках она составляет 1—1,5 об/с, в тройных — более 2 об/с.
Увеличение угловой скорости тела при отрыве происходит вследствие увеличения скорости вращения тела в толчке и предшествующих толчку тройках, переступаниях, подталкиваниях. Повышение начальной угловой скорости приводит к увеличению доли поворота тела в опорных условиях — в толчке и приземлении. Так, в двойном прыжке в безопорных условиях фигурист совершает около 1,4 оборота (550°), а 0,4 оборота (220°)—в опорных условиях, из них в толчке около 160°, а в приземлении около 60°. В однотипном тройном прыжке на долю безопорной фазы приходится около 2,25 оборота. Оставшиеся 3/4 оборота распределяются между толчком и приземлением: приблизительно 180° при отрыве и 90° при приземлении.
Вследствие увеличения начальной угловой скорости и более плотной группировки приобретается максимальная скорость. В прыжках в 3 оборота она достигает 4—4,5. об/с, а в прыжках в 3,5 и 4 оборота — примерно 5 об/с.
Важное значение имеет момент достижения максимального значения угловой скорости. При стремлении к прыжку с наибольшим числом оборотов максимальная скорость вращения должна быть достигнута возможно раньше. Лучшие исполнители прыжков в 3, 3,5 и 4 оборота достигают ее в первой половине полета. Это позволяет увеличить среднюю угловую скорость вращения и создать возможность для выполнения наибольшего числа оборотов.
ВЗАИМОДЕЙСТВИЕ КОНЬКА СО ЛЬДОМ
Характер взаимодействия конька со льдом зависит от трех основных факторов: силы трения, положения вектора силы тяжести тела относительно опорного конька и сгибательно-разгиба-тельных движений толчковой ноги. Надежная связь конька со льдом является решающим обстоятельством, обеспечивающим уверенность и стабильность движений фигуриста. Особое значение она приобретает в моменты отрыва от льда в многооборотных прыжках. Здесь надежная связь конька со льдом обеспечивается стопором, резко увеличивающим силу трения, положением тела, близким к вертикальному, при котором линия действия силы тяжести проходит вблизи опоры, а также активным разгибанием тазобедренного, коленного и голеностопного суставов, значительно увеличивающим величину опорной реакции и акцентирующим стопорящее движение.
Взаимодействие конька со льдом в процессе толчка в значительной степени зависит и от маховых движений конечностями и туловищем. Эти движения влияют на величину опорной реакции и должны быть согласованы с другими движениями в толчке, в первую очередь со сгибанием и разгибанием толчковой ноги. Маховые движения можно считать согласованными, если они дополнительно загружают толчковую ногу перед началом ее активного разгибания и уменьшают нагрузку на нее к концу толчка.
На практике надежная связь конька со льдом ощущается спортсменом как «удобство толчка», попадание в толчок, что положительно влияет на исполнение прыжка в целом, особенно на его высоту, начальное вращение и устойчивость тела в полете.
Амортизационная перегрузка. В начальный момент приземления на тело фигуриста действует сила, называемая амортизационной перегрузкой— Fam. Эта сила возникает в результате того, что перед началом приземления тело фигуриста обладает некоторой величиной кинетической энергии (энергии движения). В конце фазы амортизации величина кинетической энергии движения по вертикали равна нулю, т. е. вертикальная составляющая скорости тела (VB) уменьшается до нуля. Процесс погашения вертикальной составляющей скорости полета сопровождается появлением дополнительной нагрузки на опорно-двигательный аппарат фигуриста. Средняя величина амортизационной перегрузки может быть приближенно определена по формуле:
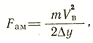
где m — масса тела фигуриста, VB — вертикальная составляющая скорости центра тяжести тела перед приземлением, Δу — вертикальное перемещение центра тяжести тела при амортизации.
Анализ выражения для Fam позволяет сделать один важный практический вывод: увеличение Δу позволяет уменьшить величину амортизационной перегрузки. Вот почему оптимальным следует считать приземление на вытянутый носок конька, что увеличивает путь амортизации и таким образом уменьшает величину амортизационной перегрузки.
 |
| Рис. 10. Направление движения центра тяжести тела и конька в приземлении |
При скольжении центр тяжести тела движется параллельно полозу конька или в направлении близком к параллельному (рис. 10). Приближенно считая, что траектории центра тяжести тела и конька опорной ноги тождественны, можно выявить связь между параметрами движения тела перед приземлением и параметром скольжения в приземлении — радиусом дуги приземления R:
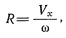
где Vx — горизонтальная составляющая скорости тела перед приземлением, ω — угловая скорость тела перед приземлением.
Чем больше радиус дуги приземления, т. е. чем положе выезд, тем он качественнее и надежнее. Значит, для улучшения качества /приземления следует стремиться увеличивать горизонтальную скорость движения тела в полете и уменьшать остаточную угловую скорость вращения.
Результаты биомеханических исследований, выраженные в числовых параметрах и систематических зависимостях, очень важны. Однако их нельзя считать самоцелью. Конечный результат предполагает соединение, осмысливание этих промежуточных данных на основе педагогических наблюдений и экспериментов. На основе такого синтеза могут быть созданы новые способы выполнения движений, новые упражнения, средства и методы тренировки.
| 
